Antonio Zoratto Sanvicente
[email protected]
12 de setembro de 2023
A aplicação do CAPM (capital asset pricing model) em exercícios de valuation de ações, por exemplo, requer a estimação do coeficiente de risco sistemático (“beta”) de cada ação que esteja sendo avaliada.
Em consequência da derivação do modelo, o coeficiente beta é definido pelo quociente entre a covariância dos retornos da ação com os retornos de um índice de mercado e a variância dos retornos do índice de mercado.
Na prática, a estimação do coeficiente é costumeiramente efetuada por meio de regressão linear entre excedentes de retorno, da ação e do índice. Por sua vez, os excedentes de retorno são as diferenças entre os retornos da ação e do índice sobre a rentabilidade do que seja adotado como representante do ativo livre de risco.
Ou seja, estima-se, com série de retornos históricos, a seguinte equação de regressão linear:
rj,t – rf,t = aj + bj(rm,t – rf,t) + ej,t
Onde:
rj,t = taxa de retorno da ação j no período t (um dia, uma semana, um mês, um ano);
rf,t = taxa de retorno do ativo livre de risco f no mesmo período t;
rm,t = taxa de retorno do índice de mercado m no mesmo período t;
ej,t = termo erro da equação de regressão da ação j no período t
Os valores dos coeficientes aj e bj são obtidos com a estimação da equação. Em especial, o valor calculado de bj é a estimativa do beta da ação j no período amostral utilizado.
Em artigo publicado no Journal of Financial Economics no ano de 1968, Myron Scholes e Joseph Williams argumentaram que há um problema econométrico relevante no procedimento acima, que costuma ser feito com o método de “mínimos quadrados ordinários”. O problema seria o seguinte: para que o estimador em questão seja não-enviesado, a variável independente, a saber, o excedente de retorno do índice de mercado, não poderia ser observada com erro. Se é observada com erro, temos o problema econométrico chamado de “erro nas variáveis”, que torna enviesado o estimador de mínimos quadrados ordinários.
E por que haveria erro? Resposta: porque os retornos da ação e do índice utilizados na prática não são observados simultaneamente. E isso ocorre porque, sendo usadas cotações de fechamento no dia (semana, mês ou ano), é bem provável que o último negócio da ação no período ocorra algum tempo antes do fechamento do índice. Ou seja, o índice continua variando, e a ação não; portanto, não se pode mais dizer que o índice estaria “causando” a ação.
Portanto, na prática os dados de retorno não estariam “sincronizados”, e essa falta de sincronização tenderia a se agravar quanto menor fosse a liquidez ou frequência de negociação da ação.
Para mitigar o problema, Scholes e Williams desenvolveram um estimador alternativo, dito “estimador de variáveis instrumentais”, permitindo o ajuste por falta de sincronização de retornos na estimação de betas.
O procedimento então proposto é o seguinte: devem ser estimados, também por mínimos quadrados ordinários, os valores de três coeficientes beta distintos, a saber:
bj,t = coeficiente obtido com retornos da ação j e do índice m nas mesmas datas t;
bj,t-1 = coeficiente obtido com retornos da ação j, na data t, e retornos do índice defasados, ou seja, observados na data t-1;
bj,t+1 = coeficiente obtido com retornos da ação j, na data t, e retornos do índice adiantados, ou seja, observados na data t+1.
A seguir, esses três betas são somados, e o resultado é dividido por um mais duas vezes o valor do coeficiente de autocorrelação do índice, ou seja, [1 + 2*correlação(rm,t; rm,t-1)].
O procedimento foi aplicado a uma amostra de ações de 16 empresas negociadas na B3, com dados diários de final do 2021 ao final de 2022. O índice de mercado foi representado pelo Ibovespa, e a taxa livre de risco correspondeu à variação diária do valor acumulado da taxa Selic. Todos os dados estão disponíveis na Economatica, não sendo necessário software econométrico especial, pois as regressões previstas podem ser realizadas em Excel.
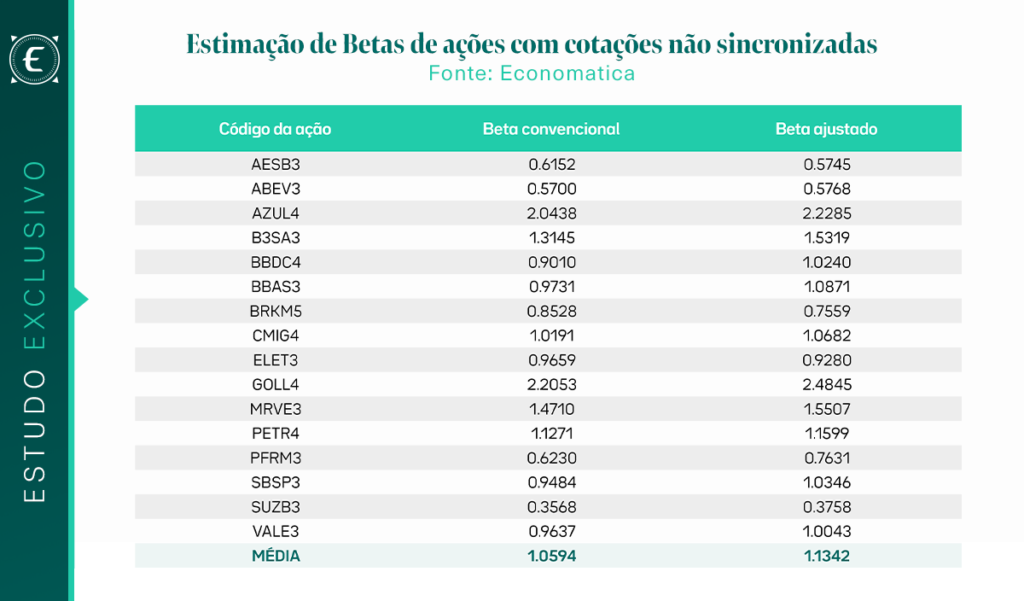
O resultado obtido foi o seguinte, notando-se que, inicialmente, são fornecidos os valores alcançados com o procedimento convencional, ou seja, sem ajuste por falta de sincronização, seguindo-se, à sua direita, os valores obtidos com a aplicação do procedimento proposto por Scholes e Williams.
Alguns comentários parecem ser apropriados.
Em primeiro lugar, o termo “beta ajustado”, no caso presente, não tem a ver com cálculo fornecido, por exemplo, em terminais Bloomberg. Ali, o ajuste efetuado o é pelo fenômeno de “reversão à média” e não por falta de sincronização de retornos.
Em segundo lugar, é esperado que o procedimento convencional, envolvendo um estimador enviesado, apresente um viés para a geração de estimativa mais baixa do que a estimativa ajustada. Tal se verifica nos resultados acima, pois pode ser visto que a média dos resultados pelo procedimento convencional (1.0594) é inferior à dos betas ajustados (1.1342). Além disso, os betas ajustados estimados são mais altos em 14 dos 16 casos analisados, sendo as exceções as ações AESB3 e BRKM5.
Em terceiro lugar, é possível dar uma ideia do impacto econômico da diferença encontrada. Suponhamos, para ilustrar, que a ação que esteja sendo avaliada seja a de uma empresa que produz USD 100 milhões de fluxo de caixa estimado em perpetuidade, sem crescimento, para o acionista. Essa projeção estaria sendo feita no final de 2022.
Sendo a taxa livre de risco igual a 3.75% (taxa corrente de US T-notes de 10 anos, no final de 2022), e o prêmio por risco de mercado de 11.72% (baseado no método implícito, conforme método em material divulgado em Economatica Insights em junho de 2023), as taxas de desconto obtidas com os dois enfoques alternativos seriam, com os valores médios informados na tabela acima:
• Com o beta não ajustado: 3.75% + 1.0594(11.72%) = 16.17% a.a.
• Com o beta ajustado: 3.75 + 1.1342(11.72%) = 17.04% a.a.
Aplicando-se essas taxas de desconto à série perpétua projetada, os resultados de valuations alternativas seriam:
• Com o beta não ajustado: USD 100 milhões/0.1617 = USD 618.43 milhões
• Com o beta ajustado: USD 100 milhões/0.1704 = USD 586.85 milhões
Portanto, o ajuste na estimação de betas indica que o procedimento convencional teria produzido um erro de superavaliação de USD 31.58 milhões.






