Antonio Zoratto Sanvicente
20 de junho de 2023
Professor Sênior, Faculdade de Economia, Administração e Contabilidade da USP
É bastante comum que o desempenho de carteiras, como as de fundos de investimento, seja avaliado com base no Sharpe ratio. Ele consiste numa fórmula que combina a rentabilidade média da carteira por período (mensal, por exemplo) com a volatilidade da carteira no mesmo período. Ou, mais especificamente, quanto foi obtido em termos de taxa mensal de retorno com o risco assumido no período de análise, através do cálculo do desvio-padrão dos retornos menais. Especificamente, ainda, o retorno médio mensal é ajustado pelo retorno do ativo livre de risco. Portanto, o retorno médio mensal é convertido em prêmio mensal por risco.
O uso do Sharpe ratio pressupõe dois fatos que não são necessariamente verdadeiros: (a) que a distribuição de probabilidades dos retornos pode ser descrita por apenas dois parâmetros – média e desvio-padrão; e (b) que os investidores se preocupam somente com rentabilidade média e volatilidade (risco) dos retornos, ou como se diz, que têm preferências por apenas duas dimensões, ficando mais satisfeitos quanto mais alto o retorno médio, e menos satisfeitos quanto mais voláteis os retornos, pois se supõe que os investidores são avessos a risco.
O primeiro fato está associado à possibilidade de que os retornos mensais, digamos, têm distribuição normal, já que esta distribuição pode ser completamente descrita por dois momentos, ou parâmetros.
No entanto, a verdadeira distribuição dos retornos pode ter mais de um parâmetro relevante. No caso da distribuição normal, que sabemos ser simétrica em torno da média, não há assimetria. Ou seja, que o valor do terceiro momento é nulo. Além disso, na distribuição normal a curtose, relacionada ao quarto momento, tem valor igual a 3.
Tem sido constatado, em mercados de ações de vários países, que os retornos observados não parecem ter distribuição normal, pois se constata tanto assimetria quanto excesso de curtose.
Como alternativa são propostos outros indicadores de desempenho de carteiras, como o Ômega ratio, por exemplo. Ele é calculado ponderando-se os retornos observados pelas suas frequências de ocorrência e, como nele é usada toda a distribuição de retornos, todos os momentos que possam existir também são considerados.
Para calcular o seu valor, fixa-se um nível desejável de desempenho e medem-se as áreas da distribuição abaixo e acima desse nível. Quanto maior a área acima desse nível, melhor o desempenho; quanto maior a área abaixo desse nível, pior o desempenho.
Portanto, é possível ranquear carteiras de fundos em termos de Ômega ratios, assim como se faz com Sharpe ratios.
No exemplo a seguir, examina-se primeiro se a carteira do Ibovespa teve retornos que poderiam ter vindo de uma distribuição normal ou não, considerados os meses do período janeiro de 2018 a dezembro de 2022. O Sharpe ratio do Ibovespa, no período, foi igual a 0,0060 ao mês. O
resultado da análise indicou a rejeição das hipóteses de que os retornos seriam simétricos e teriam excesso nulo de curtose, ou seja, curtose igual a 3.
A seguir, é medido o desempenho, no mesmo período, de 24 fundos de ações indexados, ou seja, as carteiras mais próximas da carteira do Ibovespa. Para o cálculo do Ômega ratio fixou-se o corte para divisão entre desempenho superior e desempenho inferior no Sharpe ratio do Ibovespa (0,0060).
A tabela a seguir apresenta a lista dos 24 fundos indexados analisados e os rankings obtidos por eles tanto pelo Sharpe ratio quanto pelo Ômega ratio.
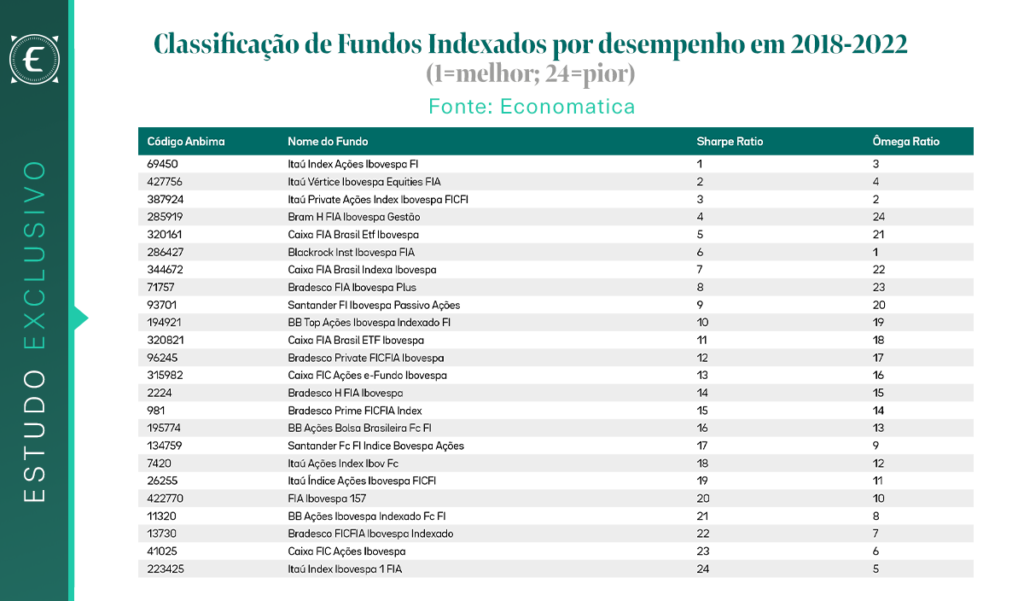
Fica claro que os rankings diferem substancialmente. Para uma conclusão mais científica, foi calculado o coeficiente de correlação por postos (rank order correlation), que usa os rankings fornecidos, e foi medida a sua significância estatística. O resultado obtido foi um coeficiente de -0,1056, o que quer dizer que as duas classificações não coincidem e, principalmente, não se pode afirmar que as duas classificações de desempenho convergem, pelo menos relativamente falando.





